Digital audio basics: audio sample rate and bit depth
Explore the science behind digital audio. Learn how sample rate and bit depth influence frequency range, noise floor, and audio resolution in music production.
In this article, we’ll cover some basic principles of digital audio and how they impact the recording and production process. Specifically, we’ll focus on audio sample rate and audio bit depth, as well as a few related topics. There's some theory and math involved, but I’ll translate into plain English and hopefully you'll understand the inner workings of digital audio a bit better. No pun intended...
Interested in trying out some of these concepts in your DAW? Start a free trial of


iZotope Music Production Suite Pro: Monthly
Common questions about sample rate and bit depth
What is sample rate in digital audio?
Sample rate refers to how many times per second an analog signal is measured. Common rates include 44.1 kHz and 48 kHz.
What does bit depth mean in audio recording?
Bit depth determines the resolution of each sample, affecting the dynamic range and noise floor of the recording.
How does a higher sample rate affect audio quality?
A higher sample rate captures more audio detail, particularly at higher frequencies, but increases file size and CPU usage.
Why is bit depth important for audio quality?
Bit depth impacts how precisely the amplitude of a signal is measured. Higher bit depths offer more dynamic range and less distortion.
What sample rate and bit depth should I use for recording?
For most music production, 44.1 kHz at 24-bit is standard. For video, 48 kHz is often preferred.
What is digital audio?
Digital audio is a representation of sound, recorded or converted into a string of binary digits – or bits – that can be stored, processed, and played back on a computer. During the analog to digital conversion process, the amplitude of an analog sound wave is captured at a specified interval, known as the sample rate. It is then “quantized” to one in a set of discrete levels determined by the bit depth.
In other words, thousands of times every second, the amplitude – a.k.a. level, loudness – of the analog sound wave is sampled, measured, and stored. Analog sound waves are continuous and infinitely variable, but because we can’t store infinitely small values with the finite number of digits we have in a computer, we round the measured amplitude to the nearest available value.
Sample rate, bit depth, and audio “resolution”
When discussing the basics of digital audio, it’s not uncommon to hear analogies drawn to video, perhaps because that’s something many people are broadly familiar with. Usually, it goes something like this: “the sample rate in digital audio is a lot like the frame rate in video, and the bit depth is like the screen resolution.”
While that does convey some of the basic principles in ways people may be familiar with, it’s actually a rather problematic analogy. Here’s why. Most people somewhat intuitively understand that in video, higher frame rates produce smoother motion and higher screen resolution produces more detailed images. Based on the analogy they’ve been given, they then understandably superimpose this onto audio: higher sample rates mean a smoother signal, and higher bit depths mean increased detail.
Here’s the problem: that’s not what sample rate or bit depth affect in digital audio. Beyond the comparison between sampling frequency and frame rate, and the “size” of each sample or frame, the analogy completely breaks down. Sure, we can reasonably say that audio with a higher sample rate and bit depth is “higher resolution,” but it just doesn’t mean the same thing as it does for video.
So what effect do sample rate and bit depth have on digital audio? I’m glad you asked! It’s actually surprisingly simple, so let’s get into it.
What is an audio sample rate?
Sample rate is the number of samples, per second, that are taken of an audio waveform to create a discrete digital signal. The higher the sample rate, the more snapshots you capture of the audio signal. The audio sample rate is measured in kilohertz – kHz – and it determines the range of frequencies captured in digital audio, specifically what the highest possible frequency is.
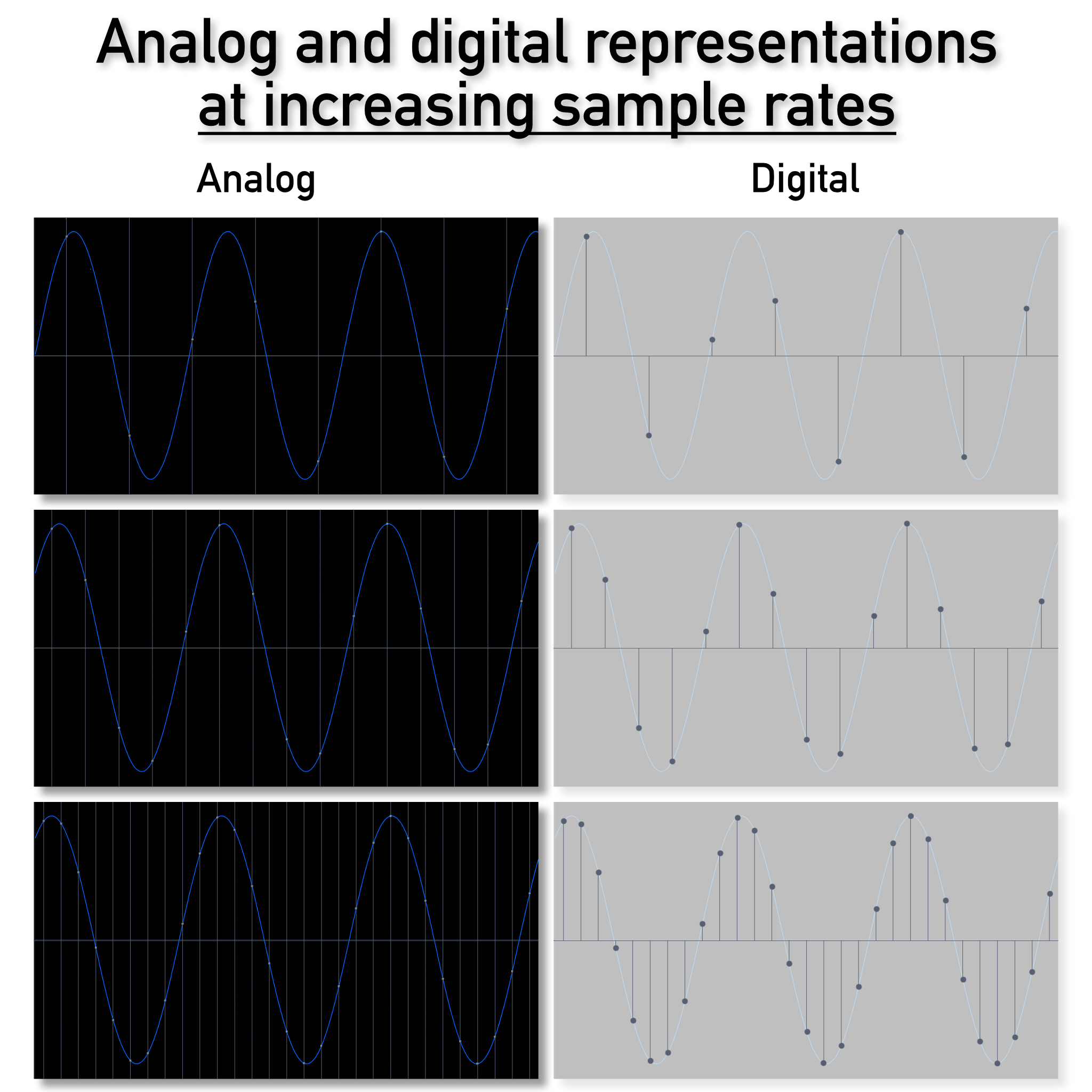
Analog and digital representations of a sine wave at increasing sample rates
I want to pause and reinforce that for a moment: the sample rate of digital audio determines the highest frequency you can capture and reproduce, and that’s it.
If you follow the film analogy, intuition might lead you to believe that even at lower frequencies, a higher sample rate would give you a smoother, more accurate representation of the waveform – and even the image above seems to suggest that – but this simply isn’t so. It’s where analogy and intuition start to break down. To a digital-to-analog converter, the three digital representations above are identical and produce exactly the same analog output. More on this shortly.
Selecting an audio sample rate
In most DAWs, you’ll find an adjustable sample rate setting in your audio preferences. This controls the sample rate for audio in your project.The options you see in the average DAW — 44.1 kHz, 48 kHz, 88.2 kHz, 96 kHz, etc. — may seem a bit random, but they aren’t!
Sample rates aren't arbitrary numbers. The relationship between sample rate and the highest frequency that can be captured and reproduced is in fact quite simple: to capture a given frequency – let’s call it ƒ – the sample rate just needs to be 2*ƒ. So, if we accept that the upper limit for human hearing is 20 kHz – although to be honest that’s generous for most people over the age of 15 or 20 – then we need a sample rate of at least twice that, or 40 kHz.
If 40 kHz sounds familiar, that may be because it’s close to one of the most common audio sample rates of 44.1 kHz. A 44.1 kHz sample rate technically allows for audio frequencies up to 22.05 kHz to be recorded, so why the extra room above 20 kHz?
Sample rates and aliasing
One of the fundamental “laws” of digital audio is related to that 2*ƒ thing – a virtual “other side of the coin,” if you will. If the highest frequency we want to record – ƒ, sometimes called the Nyquist frequency – requires a sample rate of 2*ƒ, what happens if we try to record a frequency higher than ƒ with that sample rate? In short, something called aliasing.
Aliasing is a type of digital distortion, and the way to avoid it is by “bandlimiting” the audio signal before we convert it to digital. Bandlimiting just means restricting the range of frequencies in a signal to a set upper limit, and it is done by using a low-pass filter to remove frequencies above that limit, ƒ. If we wanted to record frequencies up to 20 kHz but chose 40 kHz as our sample rate, we would have to instantly eliminate all frequencies above 20k using a so-called “brick wall” low-pass filter.
In the early days of digital, this simply wasn’t possible, and even though it is today, it tends to sound a bit unnatural. However, by shifting the Nyquist frequency above our hearing range, we can use gentler filters to eliminate aliasing without impacting the audible frequency range.
What sample rate should I record at?
When recording, mixing, and mastering, it's generally advantageous to work at a slightly higher sample rate than you think you need. Think of it as a bit of a safety net. This makes sample rates between 44.1 and 96 kHz great options for music. If you’re planning on doing some extreme downward pitch shifting or other sound design, 176.4 or 192 kHz may even be appropriate, but higher isn’t always better.
Another consideration is what sample rate you will want to use for distribution. However, these days we have excellent tools like RX to perform sample rate conversion which is easily incorporated into the mastering process.
44.1 kHz vs. 48 kHz
There was a time when 44.1 kHz was the standard for music – driven by the CD specification – while 48 kHz was used for audio tied to video. These days, however, many streaming services are capable of serving lossless audio at sample rates of up to 192 kHz. Additionally, many bluetooth devices default to 48 kHz. As such, a sample rate of 48 kHz is becoming a bit of a de-facto minimum standard for music as well.
88.2 kHz vs. 96 kHz
While 44.1 and 48 kHz are sometimes known as the “single” rates, 88.2 and 96 kHz are the so-called “double” rates. Since they contain twice as many samples for a given duration, they necessarily take up twice as much disk space, and require twice the computational power to process. But it’s 2024; disk space is cheap and computers are wicked powerful. If you don’t mind the space and processing tradeoff, the double rates give you some benefits when it comes to non-linear processing – like saturation and compression – in particular.
176.4 vs. 192 kHz
The “quad” rates of 176.4 and 192 kHz can have some applications in specific circumstances, but as mentioned earlier, higher isn’t always better. The fundamental problem has to do with measuring the voltage of the analog signal we’re trying to digitize. Specifically, it has to do with how long we have to measure that voltage.
At 44.1 kHz, a sample is taken every 22.7 microseconds (µs), or thousandths of a millisecond. At 96 kHz that shrinks to just 10.4µs. But at 192 kHz we have only 5.4µs to measure the voltage level. That’s 5.4 millionths of a second, and it’s not trivial! In short, the less time we have to measure the voltage, the less precise our measurement can be. As such, recording at quad rate can introduce its own type of distortion. For much more technical detail on this subject, I highly recommend Dan Lavry’s white papers on sampling theory and optimal sample rate.
All that said, there are still valid applications for 176.4 and 192 kHz sample rates. For example, if you’re recording tarsiers – tiny primates that use ultrasonic vocalizations to communicate – or want to do some extreme downward pitch shifting or other sound design. Still, unless you have a very specific application that requires an 80 to 90 kHz bandwidth, these quad rates – and above – are probably overkill.
Can you hear the difference between audio sample rates?
Some experienced engineers may be able to hear the differences between sample rates. However, as filtering and analog/digital conversion technologies have improved, it has become more difficult to hear these differences. Not only that, the differences you may hear are much more likely attributable to the different low pass filters used at different sample rates, not any genuine ability to hear content above 20kHz.
What is bit depth in audio?
The audio bit depth of a file determines a few things. Most directly, it determines the number of possible discrete amplitude values we can utilize for each audio sample. The higher the bit depth, the more amplitude values are available per sample. More to the point though, it determines the noise floor of the system.

Again, let’s pause to reinforce this. The bit depth of digital audio determines how low the noise floor is. Not how detailed the recording is, or how big the “stair-steps” in the digital signal are – those don’t actually exist, despite a lot of images that suggest they do. Again, even in the illustration above, the apparent stair-steps are a bit of an illusion. We’ll get more into the details of why this is so shortly.
In digital audio, there are two types of bit depth: fixed-point and floating-point. The most common fixed-point audio bit depths are 16-bit and 24-bit, and the most common floating-point format is 32-bit. As an aside, you may also sometimes hear bit depth referred to as “word length.”
Next, I want to run through a little of the math that gets us from bit depth to corresponding noise floor, showing you some of the key values you’re likely to encounter or hear about along the way. Let’s start with how we get from bit depth to the number of discrete values, or steps, that we can quantize an analog voltage to.
The formula for this is 2X, where X is a fixed point bit depth. A quick demonstration of this: 1 bit – 21 – can be 0 or 1 representing 2 values; 2 bits – 22 – can be 00, 01, 10, or 11 representing 4 values. The pattern continues. For 16 and 24 bits, the numbers work out as follows.
- 16-bit: 65,536 values
- If this were a stack of paper with each sheet representing 1 step, it would be nearly 22 feet tall.
- 24-bit: 16,777,216 values
- This would be a stack of paper over 5,592 feet tall!
Because 32-bit is a floating point bit depth, the math works a little differently. I won’t go into detail here, but if you’re interested you can read more about it on this page. What we can say about 32-bit floating point is that it has a dynamic range of 1,528 dB, 770 dB of which are above 0dBFS. We could also say that that’s equivalent to about 254 bits in fixed point, which can represent a staggering 2.8948022309×10⁷⁶ values. That’s 28,948,022,309 with another 66 zeros after it! If this were a stack of paper, not even a fraction of it would fit inside the observable universe!!
But again, that’s not quite how it actually works.
The point is this: 1,528 dB is a ludicrous amount of dynamic range.
The next interesting thing we can look at is how we get from those discrete values to what I said bit-depth actually represents: the noise floor. Like many things in digital audio, how we get there isn’t necessarily intuitive, but I’m going to try to break it down into simple steps here.
- First, we sample the analog waveform at a regular interval given by the sample rate.
- At each sample point, we measure the voltage of the analog signal.
- We then round this voltage measurement to the nearest discrete digital value. This step is known as quantization.
- This rounding introduces a signal-dependent error which, uncorrected, forms a type of distortion known as quantization noise, or quantization distortion.
- We can correct this using dither – added to the signal before quantization – which replaces the quantization distortion with uniform, low-level noise.
Because this error is never more than ½ of a step from the nearest digital value, we can calculate the level of the error relative to the full-scale signal. This is also closely tied to the level of dither noise needed to sufficiently randomize the signal. The formula for this comes from plugging the maximum and minimum number of steps into the decibel formula:
- Error level = 20*log(1/2X), where again X is the bit depth
- This can be estimated as 6.02 dB per bit
- For 16-bit this works out to -96.3 dBFS
- For 24-bit, it’s -144.5 dBFS
Maybe those numbers – -96 and -144 dB – feel familiar. If so, that’s because they’re commonly quoted as the dynamic range – the difference between the noise floor and clipping point – of 16-bit and 24-bit respectively. Now you know where they come from!
Can you hear the difference between audio bit depths?
You may be thinking, “Can human ears really tell the difference between 65,536 and 16,777,216, nonetheless 2.89×10⁷⁶ amplitude levels?”
This is a valid question. The noise floor, even in a 16-bit system, is incredibly low. Unless you need more than 96 dB of effective dynamic range, 16-bit is viable for the final master of a project.
However, while working on a project, it’s not a bad idea to work with a higher audio bit depth. Because higher bit depths lower the noise floor, you can also lower your recording level to leave more room before clipping occurs — also known as headroom.
For example, by going from 16-bit to 24-bit, you lower the noise floor by 48 dB. Even if you split that in half, you can get an extra 24 dB of headroom, while also lowering your signal-to-noise ratio by 24 dB. Having this extra buffer between the noise floor, your signal, and the clipping point is a good safety net while working and provides more flexibility down the line.
Lastly, it’s worth pointing out that virtually every modern audio workstation operates at 32-bit floating point internally – sometimes even 64-bit float! However, interfaces that convert from analog to digital and back still need to operate at 24-bit. So, that may leave you wondering…
What should my sample rate and bit depth be?
For music recording and production, a sample rate of 48 or 96 kHz at 24 bits is great. This strikes a nice balance between resolution, file size, and processing power.
For intermediate bounces or exports between the recording stage and your final masters – including things like multitracks, stems, and even your unmastered mix – 32-bit floating point at whatever sample rate you recorded at is great. This maintains the dynamic range of the original 24-bit recordings, plus any level adjustments or other processing, yet without any additional dither – or worse.
The sample rate and bit depth of your final masters will necessarily depend on your distribution medium, but these days the short version is:
- 16-bit, 44.1 kHz for CDs
- 24-bit, at the sample rate of your recording/mix/master for just about everything else
- Check with your aggregator to make sure they accept hi-res files
Start using sample rate and bit depth more effectively
Understanding the fundamentals of digital audio is key to making informed decisions in music production. In this article, we took an admittedly deep-dive into core concepts like sample rate and bit depth, unraveling how they influence the recording, mixing, and mastering process.
Sample rate determines the highest frequency that can be captured, while bit depth sets the noise floor and dynamic range of a recording. By exploring practical questions — such as “What sample rate should I use?” or “Can you hear the difference between bit depths?” — we hope we offer clear guidance for those of you navigating these technical parameters.
Complex as it may seem, the takeaway is simple: while higher sample rates and bit depths offer benefits like reduced aliasing and greater dynamic range, more isn’t always better. For most projects, 48 or 96 kHz at 24-bit strikes an excellent balance between quality, file size, and processing power. Ultimately, understanding these principles enables you to tailor your workflow to achieve professional, polished results without unnecessary complexity. Good luck, and happy digitizing!